KeKeFund Home标签归类历史
构建推荐系统（一）
|机器学习
Word count: 2.8k|Reading time: 13 min

协同型过滤 ( Collaborative filtering)
一个协作型过滤算法通常的做法是对一大群人进行搜索，并从中找出与我们品味相近的一小群人。算法会对这些人所偏爱的其他内容进行考查，并将它们组合起来构造出一个经过排名的推荐列表。

一、相似度评价方法

0，数据集

本文中的数据集都是以嵌套字典的形式出现，如下：
字典的key为用户名，value为对各个物品的评价分数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
users={'Lisa Rose': {'Lady in the Water': 2.5, 'Snakes on a Plane': 3.5,
 'Just My Luck': 3.0, 'Superman Returns': 3.5, 'You, Me and Dupree': 2.5,
 'The Night Listener': 3.0},
'Gene Seymour': {'Lady in the Water': 3.0, 'Snakes on a Plane': 3.5,
 'Just My Luck': 1.5, 'Superman Returns': 5.0, 'The Night Listener': 3.0,
 'You, Me and Dupree': 3.5},
'Michael Phillips': {'Lady in the Water': 2.5, 'Snakes on a Plane': 3.0,
 'Superman Returns': 3.5, 'The Night Listener': 4.0},
'Claudia Puig': {'Snakes on a Plane': 3.5, 'Just My Luck': 3.0,
 'The Night Listener': 4.5, 'Superman Returns': 4.0,
 'You, Me and Dupree': 2.5},
'Mick LaSalle': {'Lady in the Water': 3.0, 'Snakes on a Plane': 4.0,
 'Just My Luck': 2.0, 'Superman Returns': 3.0, 'The Night Listener': 3.0,
 'You, Me and Dupree': 2.0},
'Jack Matthews': {'Lady in the Water': 3.0, 'Snakes on a Plane': 4.0,
 'The Night Listener': 3.0, 'Superman Returns': 5.0, 'You, Me and Dupree': 3.5},
'Toby': {'Snakes on a Plane':4.5,'You, Me and Dupree':1.0,'Superman Returns':4.0}}


critics={'Lisa Rose': {'Lady in the Water': 2.5, 'Snakes on a Plane': 3.5, 
'Just My Luck': 3.0, 'Superman Returns': 3.5, 'You, Me and Dupree': 2.5, 'The Night Listener': 3.0},
'Gene Seymour': {'Lady in the Water': 3.0, 'Snakes on a Plane': 3.5, 'Just My Luck': 1.5, 
'Superman Returns': 5.0, 'The Night Listener': 3.0, 'You, Me and Dupree': 3.5},
'Michael Phillips': {'Lady in the Water': 2.5, 'Snakes on a Plane': 3.0, 
'Superman Returns': 3.5, 'The Night Listener': 4.0},
'Claudia Puig': {'Snakes on a Plane': 3.5, 'Just My Luck': 3.0, 'The Night Listener': 4.5, 
'Superman Returns': 4.0, 'You, Me and Dupree': 2.5},
'Mick LaSalle': {'Lady in the Water': 3.0, 'Snakes on a Plane': 4.0, 'Just My Luck': 2.0, 
'Superman Returns': 3.0, 'The Night Listener': 3.0, 'You, Me and Dupree': 2.0},
'Jack Matthews': {'Lady in the Water': 3.0, 'Snakes on a Plane': 4.0, 'The Night Listener': 3.0, 
'Superman Returns': 5.0, 'You, Me and Dupree': 3.5},
'Toby': {'Snakes on a Plane':4.5,'You, Me and Dupree':1.0,
'Superman Returns':4.0}}

1，曼哈顿距离

最简单的距离计算方式是曼哈顿距离。在二维模型中，每个人都可以用(x, y)的点来表示，这里我用下标表示不同的人，(x1,y2)表示艾米，(x2,y2)表示神秘的X先生，那么他们之间的曼哈顿距离就是

Python实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def sim_manhattan(rating1, rating2):

    """
    计算曼哈顿距离。
    :param rating1: 形如{'The Strokes': 3.0, 'Slightly Stoopid': 2.5}
    :param rating2: 形如{'The Strokes': 3.0, 'Slightly Stoopid': 2.5}
    """

    distance = 0
    for key in rating1:
        if key in rating2:
            distance += abs(rating1[key] - rating2[key])

    return distance

2，欧几里德距离

对于二维模型，计算的是两点之间的直线距离。

对于N维模型，如下表：

@ | Angelica | Bill
-|-
Blues Traveler | 3.5 | 2
Broken Bells | 2 | 3.5
Deadmau5 | - | 4
Norah Jones | 4.5 | -
Phoenix | 5 | 2
Slightly Stoopid | 1.5 | 3.5
The Strokes | 2.5 | -
Vampire Weekend | 2 | 3

计算Angelica和Bill的欧几里得距离：

$$ Euclidean = \sqrt{(3.5-2)^2 + (2-3.5)^2+(5-2)^2+(1.5-3.5)^2+(2-3)^2} = 4.3 $$

Python实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
from math import sqrt

def sim_euclidean(users, person1, person2):
    """
    欧几里得距离
    返回一个有关person1与person2的基于距离的相似度评价
    :param users:{'Lisa Rose': { 'Snakes on a Plane': 3.5,...},'Gene Seymour': {'Lady in the Water': 3.0, ...}
    :param person1: 形如'Lisa Rose'
    :param person2: 形如'Lisa Rose'
    :return:介于[0, 1]，值为1表明两个人对每一样物品均有着完全一致的评价
    """

    # 得到shared_items的列表
    shared_items = {}
    for item in users[person1]:
        if item in users[person2]:
            shared_items[item] = 1

    # 如果两者没有共同之处，则返回0
    if len(shared_items) == 0:
        return 0

    # 计算所有差值的平方和
    sum_of_squares = sum([pow(users[person1][item]-users[person2][item], 2)
                          for item in users[person1] if item in users[person2]])
    return 1/(1+sqrt(sum_of_squares))
    

dis = sim_euclidean(critics, 'Lisa Rose', 'Jack Matthews')
print dis

3, 皮尔逊相关度评价

用户的问题

让我们仔细看看用户对乐队的评分，可以发现每个用户的打分标准非常不同：

  • Bill没有打出极端的分数，都在2至4分之间；

  • Jordyn似乎喜欢所有的乐队，打分都在4至5之间；

  • Hailey是一个有趣的人，他的分数不是1就是4。

那么，如何比较这些用户呢？解决方法之一是使用皮尔逊相关系数。

该计算系数是判断两组数据与某一直线拟合程度的一种度量。对应的公式比欧几里德距离评价的计算公式要复杂，但是它在数据不是很规范的时候（比如影评者对影片的评价总是相对于平均水平偏离很大时），会倾向于给出更好的结果。

我们先看下面的数据：

@ | Blues Traveler | Norah Jones | Phoenix | Strokes | Weird AI
-|-
Clara | 4.75 | 4.5 | 5 | 4.25 | 4
Robert | 4 | 3 | 5 | 2 | 1

这种现象在数据挖掘领域称为“分数膨胀”。Clara最低给了4分——她所有的打分都在4至5分之间。我们将它绘制成图表：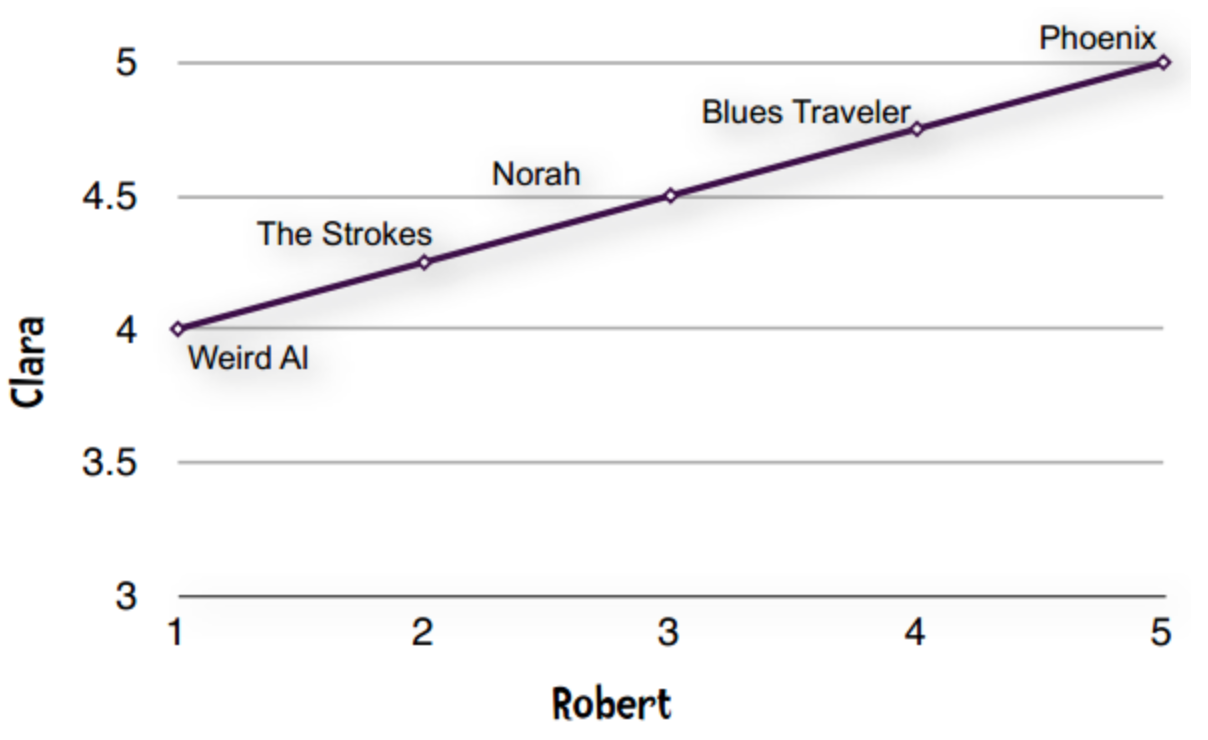

一条直线——完全吻合！！！

直线即表示Clara和Robert的偏好完全一致。他们都认为Phoenix是最好的乐队，然后是Blues Traveler、Norah Jones。如果Clara和Robert的意见不一致，那么落在直线上的点就越少。

皮尔逊相关系数的计算公式：

Python实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
def sim_pearson(users, person1, person2):
    """
    返回p1和p2的皮尔逊相关系数
    :param users:{'Lisa Rose': { 'Snakes on a Plane': 3.5,...},'Gene Seymour': {'Lady in the Water': 3.0, ...}
    :param person1: 形如'Lisa Rose'
    :param person2: 形如'Lisa Rose'
    :return: 介于[-1, 1]，值为1表明两个人对每一样物品均有着完全一致的评价
    """

    # 得到双方都曾评价过的物品列表
    shared_items = {}
    for item in users[person1]:
        if item in users[person2]:
            shared_items[item] = 1

    # 得到列表元素的个数
    n = len(shared_items)

    # 如果没有共同之处，则返回1
    if n == 0:
        return 1

    # 对所有偏好求和
    sum1 = sum([users[person1][item] for item in shared_items])
    sum2 = sum([users[person2][item] for item in shared_items])

    # 求平方和
    sum1_sq = sum([pow(users[person1][item], 2) for item in shared_items])
    sum2_sq = sum([pow(users[person2][item], 2) for item in shared_items])

    # 求乘积之和
    pSum = sum([users[person1][item] * users[person2][item] for item in shared_items])

    # 计算皮尔逊评价值
    num = pSum - (sum1*sum2/n)
    den = sqrt((sum1_sq - pow(sum1, 2)/n) * (sum2_sq - pow(sum1, 2)/n))
    if den == 0:
        return 0

    r = num/den

    return r

dis = sim_pearson(critics, 'Lisa Rose', 'Jack Matthews')
print dis

4，余弦相似度

它在文本挖掘中应用得较多，在协同过滤中也会使用到。这里记录了每个用户播放歌曲的次数，我们用这些数据进行推荐。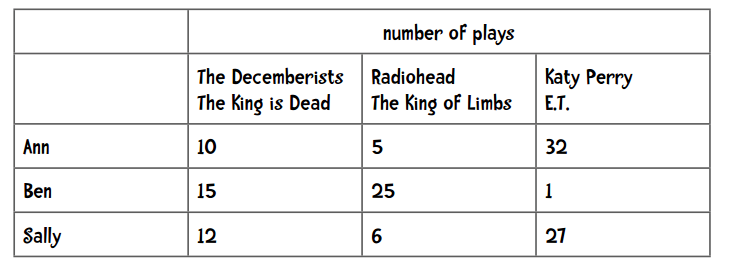

简单扫一眼上面的数据，我们可以发现Ann和Sally的偏好更为相似。

可以看到，Moonlight Sonata这首歌我播放了25次，但很有可能你一次都没有听过。事实上，上面列出的这些歌曲可能你一手都没听过。此外，iTunes上有1500万首音乐，而我只听过4000首。所以说单个用户的数据是稀疏的，因为非零值较总体要少得多。当我们用1500万首歌曲来比较两个用户时，很有可能他们之间没有任何交集，这样一来就无从计算他们之间的距离了。

余弦相似度的计算中会略过这些非零值。它的计算公式是：

$$ cos(x, y) = \dfrac{x\cdot y}{||x||\times||y||} $$

其中，“·”号表示数量积。“||x||”表示向量x的模，计算公式为:

对于下表：

@ | Blues Traveler | Norah Jones | Phoenix | Strokes | Weird AI
-|-
Clara | 4.75 | 4.5 | 5 | 4.25 | 4
Robert | 4 | 3 | 5 | 2 | 1

有两个向量：

1
2
x = (4.75, 4.5, 5, 4.25, 4)
y = (4, 3, 5, 2, 1)

它们的模是：

$$ ||x|| = \sqrt{4.75^2 + 4.5^2 + 5^2 + 4.25^2 + 4^2} = 10.09 $$

$$ ||y|| = \sqrt{4^2 + 3^2 + 5^2 + 2^2 + 1^2} = 7.416 $$

数量积的计算：

因此余弦相似度是：
$$ cos(x, y) = \dfrac{70}{10.093\times7.416} = 0.935 $$

5，应该使用哪种相似度？

  • 如果数据存在“分数膨胀”问题，就使用皮尔逊相关系数

  • 如果数据比较“密集”，变量之间基本都存在公有值，且这些距离数据是非常重要的，那就使用欧几里德或曼哈顿距离。

  • 如果数据是稀疏的，则使用余弦相似度。

二、应用

1，推荐用户 —— K最邻近算法

使用K最邻近算法来找出K个最相似的用户。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
def top_matches(users, person, k=5, similarity=sim_pearson):

    """
    从反映偏好的字典中返回最为匹配者
    返回结果的个数和相似度函数均为可选参数
    :param users:
    :param person:
    :param k:
    :param similarity:
    :return:
    """

    scores = [(similarity(users, person, other), other)
              for other in users if other != person]

    # 对列表进行排序，评价值最高者排载最前面
    scores.sort()
    scores.reverse()
    return scores[:k]

scores = top_matches(critics, 'Toby', k=3)
print scores


Output>>:[(0.9912407071619299, 'Lisa Rose'), (0.9244734516419049, 'Mick LaSalle'), (0.8934051474415647, 'Claudia Puig')]

2，推荐物品

通过一个经过加权的评价值来为影片打分，评论者的评分结果因此形成了先后的排名。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
def getRecommendations(users, person, similarity=sim_pearson):
    """
    利用所有他人评价值的加权平均，为某人提供建议
    :param users:
    :param person:
    :param similarity: 可指定相似度评价函数
    :return:
    """

    totals = {}
    simSums = {}
    for other in users:
        # 不要和自己做比较
        if other == person:
            continue

        sim = similarity(users, person, other)

        # 忽略评价值为零或者小于零的情况
        if sim <= 0:
            continue

        for item in users[other]:

            # 只对自己还未曾看过的影片进行评价
            if item not in users[person] or users[person][item] == 0:

                # 相似度 * 评价值
                totals.setdefault(item, 0)
                totals[item] += users[other][item] * sim

                # 相似度之和
                simSums.setdefault(item, 0)
                simSums[item] += sim

    # 建立一个归一化的列表
    rankings = [(total/simSums[item], item) for item, total in totals.items()]

    # 返回经过排序的列表
    rankings.sort()
    rankings.reverse()
    return rankings

rankings = getRecommendations(critics, 'Toby')
print 'pearson\n', rankings

rankings = getRecommendations(critics, 'Toby', similarity=sim_euclidean)
print 'euclidean\n', rankings


Output:

pearson
[(3.3477895267131013, 'The Night Listener'), (2.8325499182641614, 'Lady in the Water'), (2.5309807037655645, 'Just My Luck')]

euclidean
[(3.457128694491423, 'The Night Listener'), (2.778584003814924, 'Lady in the Water'), (2.4224820423619167, 'Just My Luck')]
Author: Binger Chen
Link: http://www.kekefund.com/2016/05/11/recommendation-system/
Copyright Notice: All articles in this blog are licensed under CC BY-NC-SA 4.0 unless stating additionally.
Python机器学习相似度评价